当前的Authenticated存储系统有挺大的限制：

• 只是单纯的KV存储，使用“get/set/range”很方便，但是往往在遇到“select a, b, c from FOO where a is even”那时代价很大
• 为了突破这个限制，需要一个更灵活的authenticated存储index

A more flexible authenticated storage index

在尝试过后发现还是有如下限制：

• 只能通过一个属性进行索引
  • 不能index一个有(a, b, c)格式记录的表并且通过一个key进行搜索
• 搜索路径此时证明大小（proof size）随着key长度变化
• 不能自平衡，导致了更多读写放大还有反复不定的查找路径长度

Cont

想法：用B+ Trees

• 可以index随意的属性字段并且还可以执行随意的部分查找
• 自平衡，搜索路径通常都是O(logN)
• 只需要一个类似Verkle Trees的证明方案
• 高度面向磁盘的数据结构是从80年代开始数据库系统的黄金准则
• 可以使用一些现代数据库的B-Tree优化手段：
  • 前缀编码（共享公共后缀）
  • 后缀截断（共享公共前缀）

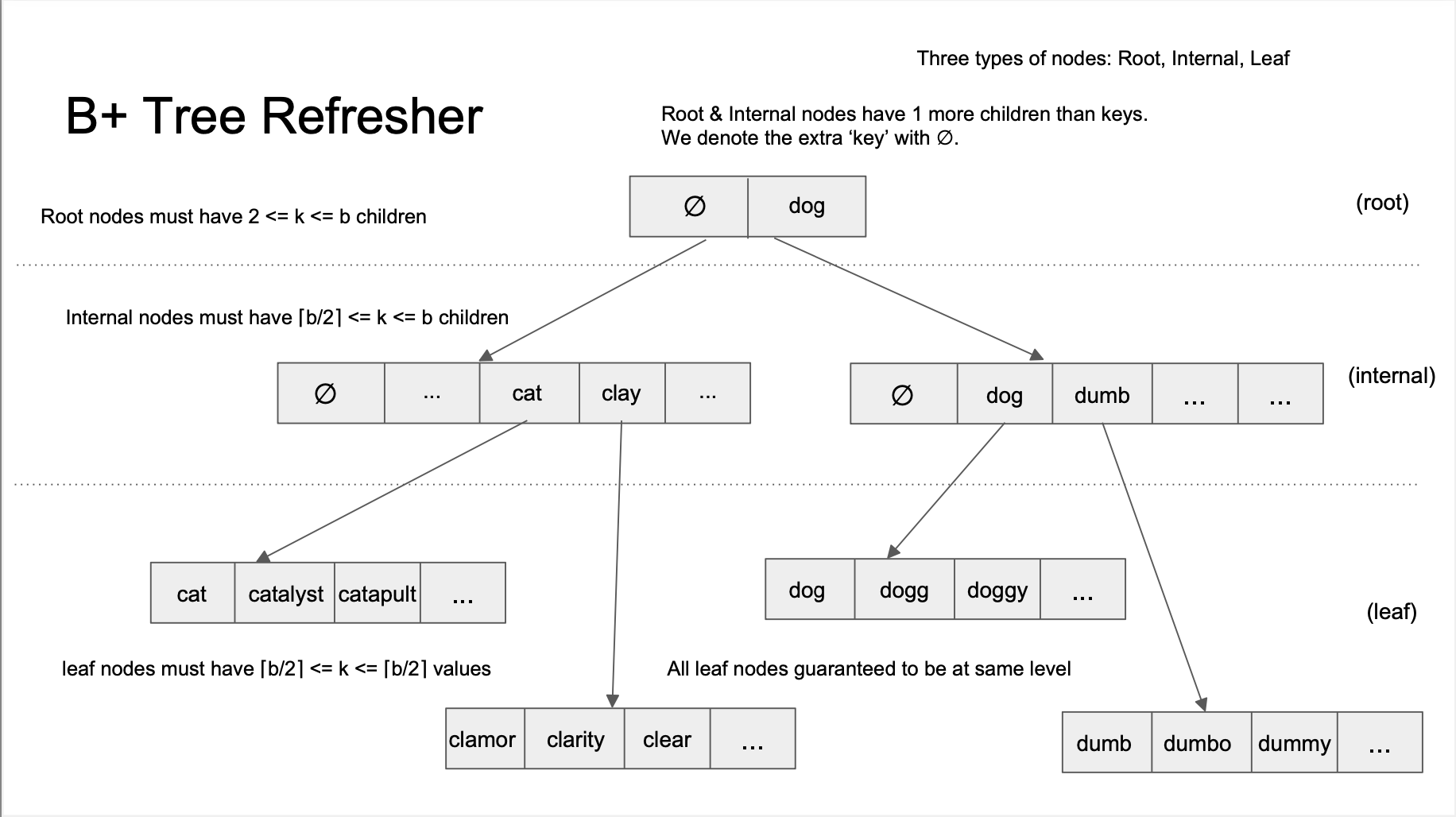
Berkle Trees

• Idea:
  • 用KZG commitments去证明parent-child关系
  • 用Dankrad's KZG多重证明去证明多批数据就像Verkle尝试一样
• Construction:
  • 每个节点都插入一个多项式 f(xi) = yi 其中
    • xi = hash(keyi || i), where keyi is the ith key in the node
    • yi = hash(value) if leaf else hash(child_commitment)
  • 为了证明parent-child关系，prover选择(xi, yi)并且给出verifier:
    • C, a KZG commitment to f
    • W, witness element for the opening f(xi) = yi

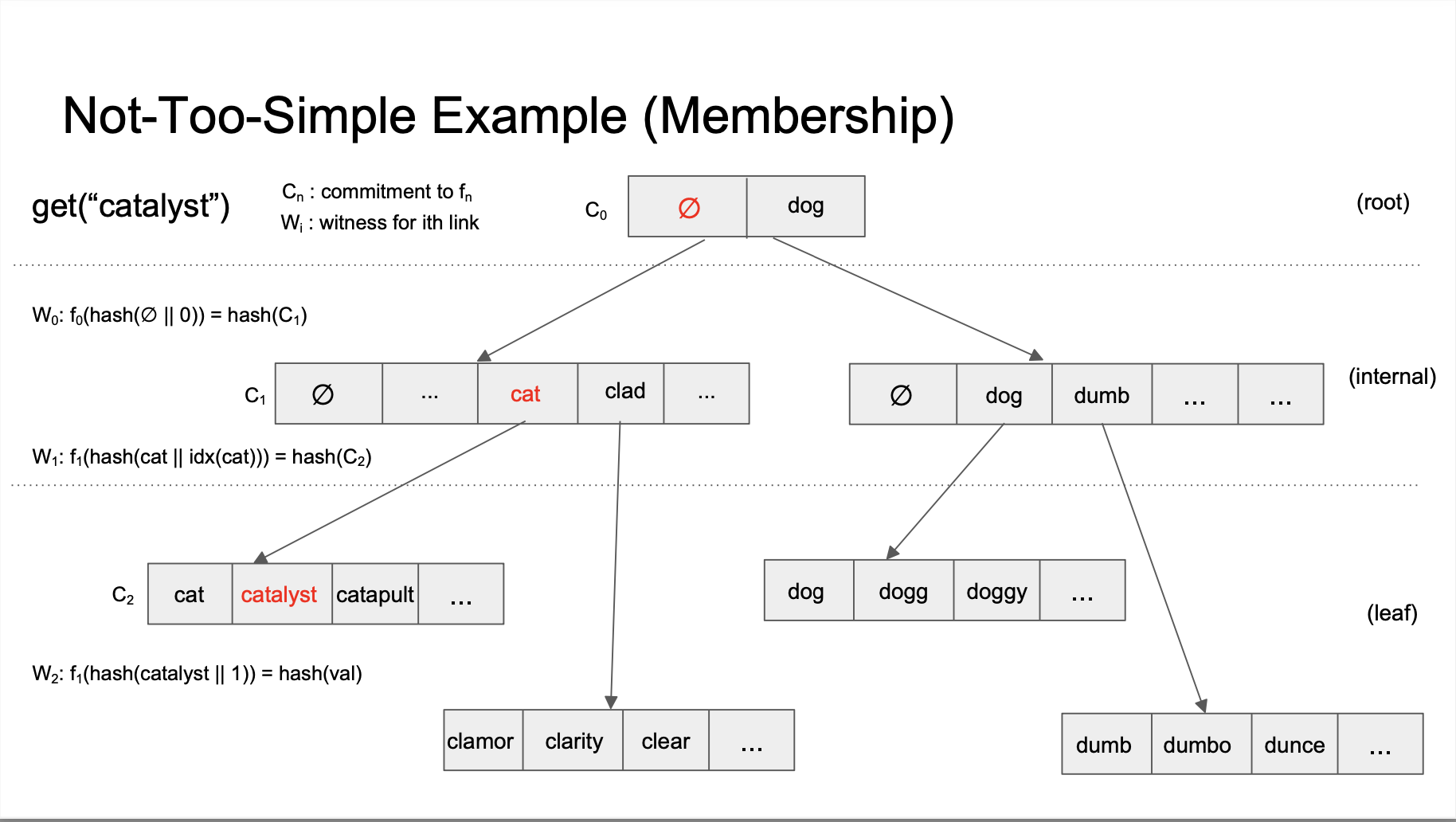
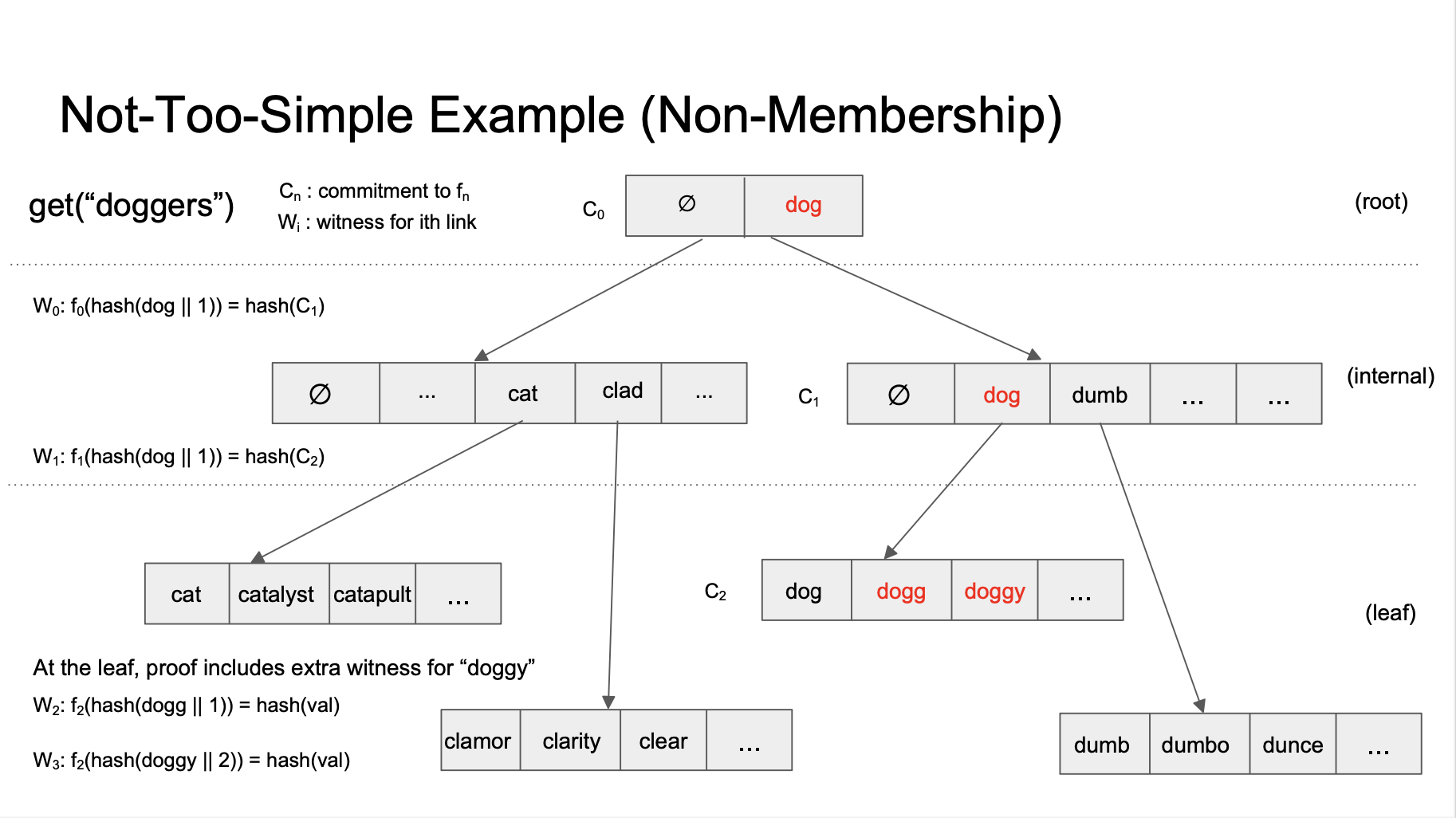
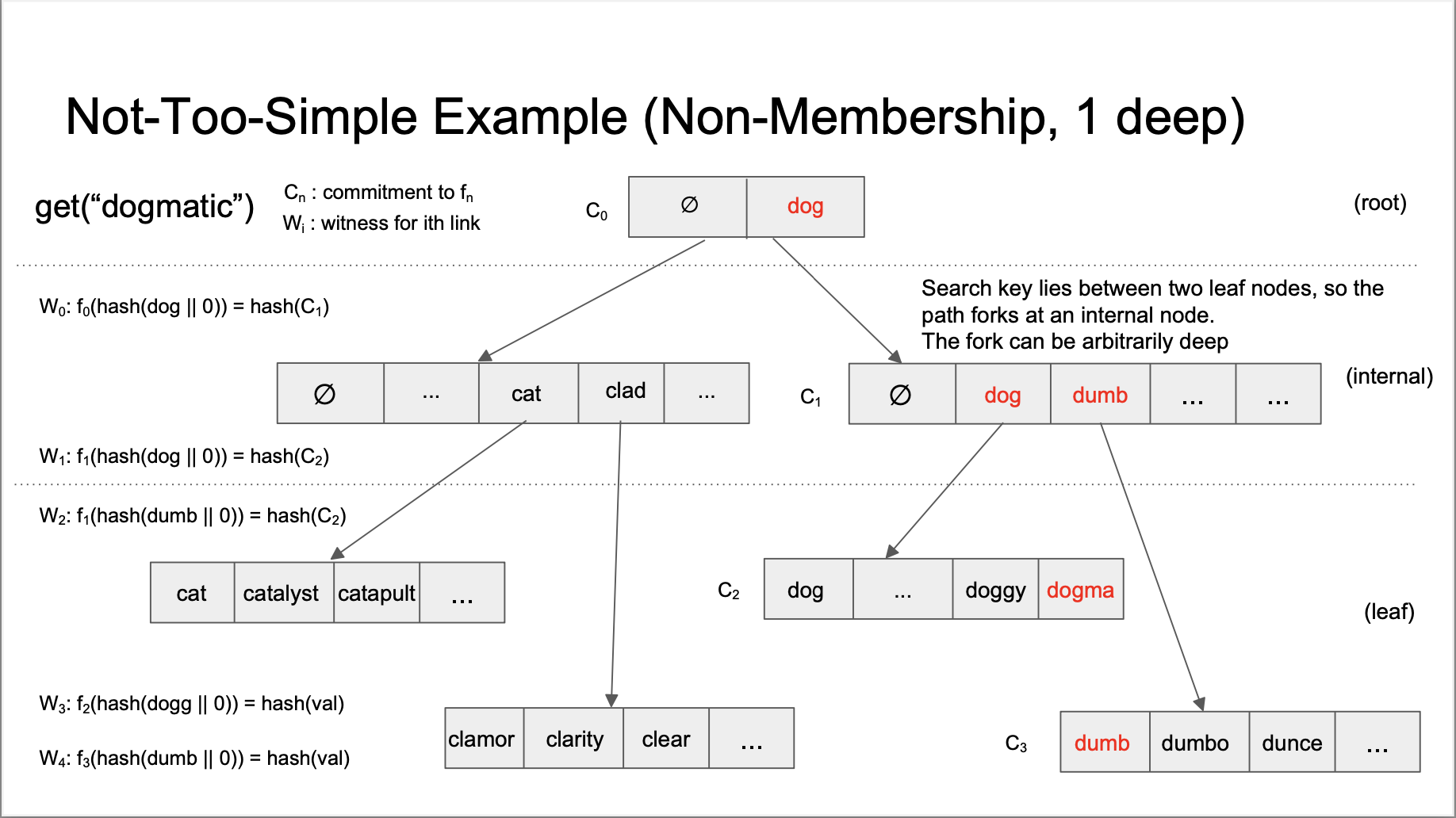
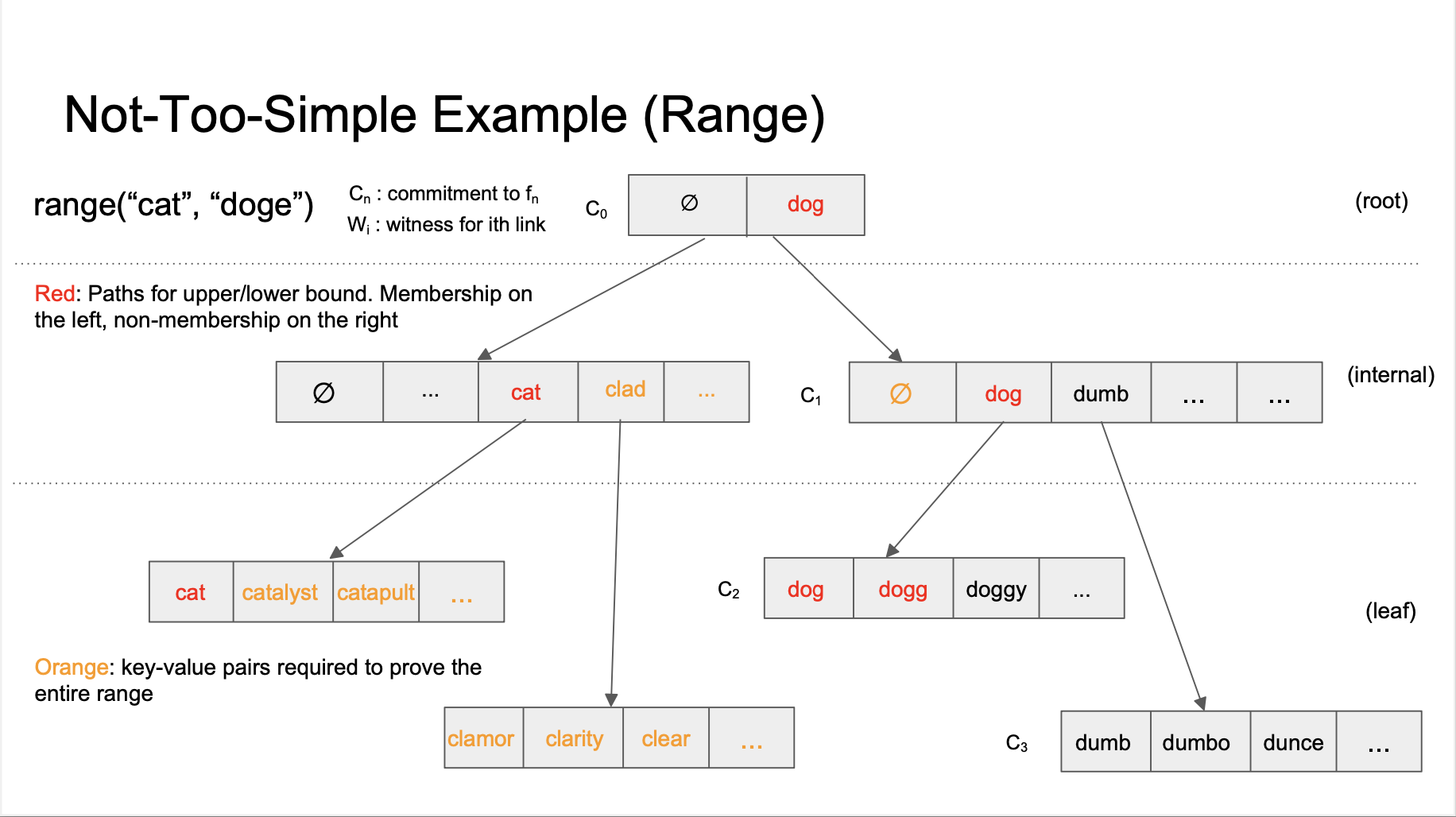
Berkle vs Verkle

• Berkle trees are very similar to Verkle tries
• Both Verkle and Berkle...
  • produces vastly smaller proofs leading to better state sync and light client performance
  • trade proof size for more expensive crytography
  • use additively homomorphic vector commitments so they're not too expensive to update
  • have large branching factors

Berkle vs Verkle (contd)

Berkle

• +Can search via arbitrary predicates
  • E.g. “SELECT a, b, c from FOO where a is even”
• +Can index multiple properties
• +Search path length is independent of key size
• +Can use all existing B+ Tree optimizations

• -Larger storage footprint than verkle
• -Proofs must contain keys along audit path*
• -Polynomial x values are larger, so they can’t be represented in evaluation form**

Verkle

• +Key is the search path, so proof doesn’t need to contain audit path keys
• +Polynomial x values are small, so they can be kept almost exclusively in evaluations form
• +Smaller storage footprint than Berkle

• -Can only perform key-value or range queries-does not support arbitrary predicates
• -Can only index a single property
• -Search path length depends on key size